Oct 06, 2019
Suppose you observe the historical returns of $p$ different fund managers,
and wish to test whether any of them have superior Signal-Noise ratio (SNR)
compared to the others.
The first test you might perform is the test of pairwise equality of all SNRs.
This test relies on the multivariate delta method and central limit theorem,
resulting in a chi-square test, as described by Wright et al and outlined
in section 4.3 of our Short Sharpe Course.
This test is analogous to ANOVA, where one tests different populations for unequal
means, assuming equal variance.
(The equal Sharpe test, however, deals naturally with the case of paired observations,
which is commonly the case in testing asset returns.)
In the analogous procedure, if one rejects the null of equal means in an ANOVA, one
can perform pairwise tests for equality. This is called a post hoc test, since
it is performed conditional on a rejection in the ANOVA.
The basic post hoc test is Tukey's range test, sometimes called 'Honest Significant Differences'.
It is natural to ask whether we can extend the same procedure to testing the SNR.
Here we will propose such a procedure for a crude model of correlated returns.
The Tukey test has increased power by pooling all populations together to
estimate the overall variance. The test statistic then becomes something like
$$
\frac{Y_{(p)} - Y_{(1)}}{\sqrt{S^2 / n}},
$$
where $Y_{(1)}$ is the smallest mean observed, and $Y_{(p)}$ is the largest,
and $S^2$ is the pooled estimate of variance. The difference between
the maximal and minimal $Y$ is why this is called the 'range' test,
since this is the range of the observed means.
Switching back to our problem, we should not have to assume that our
tested returns series have the same volatility.
Moreover, the standard error of the Sharpe ratio is only weakly dependent
on the unknown population parameters, so we will not pool variances.
In our paper on testing the asset with maximal Sharpe,
we established that the vector of Sharpes, for normal returns and
when the SNRs are small,
is approximately asymptotically normal:
$$
\hat{\zeta}\approx\mathcal{N}\left(\zeta,\frac{1}{n}R\right).
$$
Here $R$ is the correlation of returns.
See our previous blog post for more details.
Under the null hypothesis that all SNRs are equal to $\zeta_0$,
we can express this
$$
z = \sqrt{n} \left(R^{1/2}\right)^{-1} \left(\hat{\zeta} - \zeta_0\right) \approx\mathcal{N}\left(0,I\right),
$$
where $R^{1/2}$ is a matrix square root of $R$.
Now assume the simple rank-one model for correlation, where
assets are correlated to a single common latent factor,
but are otherwise independent:
$$
R = \left(1-\rho\right) I + \rho 1 1^{\top}.
$$
Under this model of $R$ we computed inverse-square-root
of $R$ as
$$
\left(R^{1/2}\right)^{-1} = \left(1-\rho\right)^{-1/2} I + \frac{1}{p}\left(\frac{1}{\sqrt{1-\rho+p\rho}} - \frac{1}{\sqrt{1-\rho}}\right)1 1^{\top}.
$$
Picking two distinct indices, $i, j$ let $v = \left(e_i - e_j\right)$ be the contrast
vector. We have
$$
v^{\top}z = \frac{\sqrt{n}}{\sqrt{\left(1-\rho\right)}}v^{\top}\hat{\zeta},
$$
because $v^{\top}1=0$.
Thus the range of the observed Sharpe ratios is a scalar multiple of the range
of a set of $p$ independent standard normal variables.
This is akin to the 'monotonicity' principle that we abused earlier
when performing inference on the asset with maximum Sharpe.
Under normal approximation and the rank-one correlation model, we should then
see
$$
\left|\hat{\zeta}_{i} - \hat{\zeta}_{j}\right| \ge HSD = q_{1-\alpha,p,\infty} \sqrt{\frac{(1-\rho)}{n}},
$$
with probability $\alpha$, where the $q_{1-\alpha,m,n}$ is the upper $\alpha$-quantile
of the Tukey distribution with $m$ and $n$ degrees of freedom.
This is computed by qtukey in R.
Alternatively one can construct confidence intervals around each $\hat{\zeta}_i$ of
width $HSD$, whereby if another $\hat{\zeta}_j$ does not fall within it, the two
are said to be Honestly Significantly Different. The familywise error rate should be
no more than $\alpha$.
Testing
Let's test this under the null. We spawn 4 years of correlated returns
from 16 managers, then compare the maximum and minimum observed Sharpe ratio,
comparing them to the test value of $HSD$.
Assume that the correlation is known to have value $\rho=0.8$.
(More realistically, it would have to be estimated.)
Note that for this many fund managers we have
$$
q_{0.95,16,\infty}=4.85,
$$
and thus taking into account the $\sqrt{1-\rho}$ term,
$$
HSD = \frac{1}{\sqrt{n}} 2.17.
$$
This is only slightly bigger than the naive approximate confidence
intervals one would typically apply to the Sharpe ratio, which in this case
would be around
$$
\frac{\Phi^{-1}\left(0.975\right)}{\sqrt{n}} = \frac{1.96}{\sqrt{n}}.
$$
We perform 10 thousand simulations, computing the Sharpe over all managers,
and collecting the ranges. We compute the empirical type I error rate,
and find it to be nearly equal to the nominal value of 0.05:
suppressMessages({
library(mvtnorm)
})
nman <- 16
nyr <- 4
ope <- 252
SNR <- 0.8 # annual units
rho <- 0.8
nday <- round(nyr * ope)
R <- pmin(diag(nman) + rho,1)
mu <- rep(SNR / sqrt(ope),nman)
nsim <- 10000
set.seed(1234)
ranges <- replicate(nsim,{
X <- mvtnorm::rmvnorm(nday,mean=mu,sigma=R)
zetahat <- colMeans(X) / apply(X,2,sd)
max(zetahat) - min(zetahat)
})
alpha <- 0.05
HSDval <- sqrt((1-rho) / nday) * qtukey(alpha,lower.tail=FALSE,nmeans=nman,df=Inf)
mean(ranges > HSDval)
Compact Letter Display
The results of Tukey's test can be difficult to summarize. You might observe,
for example, that managers 1 and 2 have significantly different SNRs,
but not have enough evidence to say that 1 and 3 have different SNR, nor 2 and 3.
How, then should you think about manager 3? He/She perhaps has the same SNR as
2, and perhaps the same as 1, but you have evidence that 1 and 2 have different SNR.
You might label 1 as being among the 'high performers' and 2 among the 'average performers';
In which group should you place 3?
One answer would be to put manager 3 in both groups.
This is a solution you might see as the result of compact letter displays, which is
a commonly used way of communicating the results of multiple comparison procedures
like Tukey's test.
The idea is to put managers into multiple groups, each group identified by a letter,
such that if two managers are in a common group, the HSD test fails to find they
have significantly different SNR.
The assignment to groups is actually not unique, and so subject to
optimizing certain criteria, like minimizing the total number of groups, and so on,
cf. Gramm et al.
For our purposes here, we use Piepho's algorithm, which is conveniently provided
by the multcompView package in R.
Here we apply the technique to the series of monthly returns of 5 industry
factors, as compiled by Ken French, and published in his data library.
We have almost 1200 months of data for these 5 returns.
The returns are highly positively correlated, and we find that their
common correlation is very close to 0.8.
For this setup, and measuring the Sharpe in annualized units,
the critical value at the 0.05 level is
$$
HSD = \sqrt{12/n} 1.73.
$$
For comparison, the half-width of the two sided confidence interval on the
Sharpe in this case would be
$$
\sqrt{12/n} 1.96,
$$
which is a bit bigger. We have actually gained resolving power in our
comparison of industries because of the high level of correlation.
Below we compute the observed Sharpe ratios of the five industries,
finding them to range from around $0.49\,\mbox{year}^{-1/2}$ to
$0.67\,\mbox{year}^{-1/2}$.
We compute the HSD threshold, then call Piepho's method and
print the compact letter display, shown below.
In this case we require two groups, 'a' and 'b'.
Based on our post hoc test, we assign
Healthcare and Other into two different groups, but find no other
honest significant differences, and so Consumer, Manufacturing and Technology
get lumped into both groups.
# this is just a package of some data:
# if (!require(aqfb.data)) { install.packages('shabbychef/aqfb_data') }
library(aqfb.data)
data(mind5)
mysr <- colMeans(mind5) / apply(mind5,2,FUN=sd)
# sort decreasing for convenience later
mysr <- sort(mysr,decreasing=TRUE)
# annualize it
ope <- 12
mysr <- sqrt(ope) * mysr
# show
print(mysr)
## Healthcare Consumer Manufacturing Technology Other
## 0.6674 0.6487 0.5967 0.5906 0.4852
srdiff <- outer(mysr,mysr,FUN='-')
R <- cov2cor(cov(mind5))
# this ends up being around 0.8:
myrho <- median(R[row(R) < col(R)])
alpha <- 0.05
HSD <- sqrt(ope) * sqrt((1-myrho) / nrow(mind5)) * qtukey(alpha,lower.tail=FALSE,nmeans=ncol(mind5),df=Inf)
library(multcompView)
lets <- multcompLetters(abs(srdiff) > HSD)
print(lets)
## Healthcare Consumer Manufacturing Technology Other
## "a" "ab" "ab" "ab" "b"
Jun 04, 2019
In a previous blog post we used the
'Polyhedral Inference' trick of Lee et al. to perform
conditional inference on the asset with maximum Sharpe ratio.
This is now a short paper on arxiv.
I was somewhat disappointed to find, as noted in the paper,
that polyhedral inference has lower power than a simple Bonferroni correction
against alternatives where many assets have the same Signal-Noise ratio.
(Though apparently it has higher power when one asset alone higher SNR.)
The interpretation is that when there is no spread in the SNR, Bonferroni
correction should have the same power as a single asset test, while
conditional inference is sensitive to the conditioning information that
you are testing a single asset which has Sharpe ratio perhaps near that of
other assets. In the opposite case, Bonferroni suffers from having to 'pay'
for a lot of irrelevant (for having low Sharpe) assets, while conditional
inference does fine.
I also showed in the paper, as I demonstrated in a previous blog post,
that the Bonferroni correction is conservative when asset
returns are correlated. In a simple simulations under the null, I showed
that the empirical type I rate goes to zero as common correlation $\rho$ goes to one.
In this blog post I will describe a simple trick to correct for average positive
correlation.
So let us suppose that we observe returns on $p$ assets over $n$ days,
and that returns have correlation matrix $R$.
Let $\hat{\zeta}$ be the vector of Sharpe ratios over this sample.
In the paper I show that if returns are normal then the following
approximation holds
$$
\hat{\zeta}\approx\mathcal{N}\left(\zeta,\frac{1}{n}\left(
R + \frac{1}{2}\operatorname{Diag}\left(\zeta\right)\left(R \odot R\right)\operatorname{Diag}\left(\zeta\right)
\right)\right).
$$
There is a more general form for Elliptically distributed returns.
In the paper I find, via simulations, that for realistic
SNRs and large sample sizes, the more general form does not add much
accuracy. In fact, for the small SNRs one is likely to see in practice
the simple approximation
$$
\hat{\zeta}\approx\mathcal{N}\left(\zeta,\frac{1}{n}R\right)
$$
will suffice.
Now note that, under the null hypothesis that $\zeta = \zeta_0$, one has
$$
z = \sqrt{n} \left(R^{1/2}\right)^{-1} \left(\hat{\zeta} - \zeta_0\right) \approx\mathcal{N}\left(0,I\right),
$$
where $R^{1/2}$ is a matrix square root of $R$.
Testing the null hypothesis should proceed by computing (or estimating) the
vector $z$, then comparing to normality, either by a Chi-square statistic,
or performing Bonferroni-corrected normal inference on the largest element.
In the paper I used a simple rank-one model for correlation for simulations
using
$$
R = \left(1-\rho\right) I + \rho 1 1^{\top}.
$$
This effectively models the influence of a common single 'latent' factor.
Certainly this is more flexible for modeling real returns
than assuming identity correlation, but is not terribly realistic.
Under this model of $R$ it is simple enough to compute the inverse-square-root
of $R$. Namely
$$
\left(R^{1/2}\right)^{-1} = \left(1-\rho\right)^{-1/2} I + \frac{1}{p}\left(\frac{1}{\sqrt{1-\rho+p\rho}} - \frac{1}{\sqrt{1-\rho}}\right)1 1^{\top}.
$$
Let's just confirm with code:
p <- 4
rho <- 0.3
R <- (1-rho) * diag(p) + rho
ihR <- (1/sqrt(1-rho)) * diag(p) + (1/p) * ((1/sqrt(1-rho+p*rho)) - (1/sqrt(1-rho)))
hR <- solve(ihR)
R - hR %*% hR
[,1] [,2] [,3] [,4]
[1,] 4.44089e-16 1.66533e-16 1.11022e-16 1.66533e-16
[2,] 1.66533e-16 0.00000e+00 5.55112e-17 5.55112e-17
[3,] 1.66533e-16 1.66533e-16 0.00000e+00 1.11022e-16
[4,] 1.11022e-16 1.11022e-16 1.11022e-16 2.22045e-16
So to test the null hypothesis, one computes
$$
z = \sqrt{n} \left( \left(1-\rho\right)^{-1/2} I + \frac{1}{p}\left(\frac{1}{\sqrt{1-\rho+p\rho}} - \frac{1}{\sqrt{1-\rho}}\right)1 1^{\top} \right)
\left(\hat{\zeta} - \zeta_0\right)
$$
to test against normality. But note that our linear transformation is monotonic (indeed affine):
if $v_i \ge v_j$ and $w = \left(R^{1/2}\right)^{-1} v$, then $w_i \ge w_j$.
This means that the maximum element of $z$ has the same index as the maximum element of
$\hat{\zeta} - \zeta_0$.
To perform Bonferroni correction we need only transform the largest element of
$\hat{\zeta} - \zeta_0$, by scaling it up, and shifting to accomodate the average.
So if the largest element of $\hat{\zeta} - \zeta_0$ is $y$, and the average value
is $a = \frac{1}{p}1^{\top} \left(\hat{\zeta} - \zeta_0\right)$, then the largest
value of $z$ is
$$
\frac{\sqrt{n} y}{\sqrt{1-\rho}} + a \sqrt{n} \left(\frac{1}{\sqrt{1-\rho+p\rho}} - \frac{1}{\sqrt{1-\rho}}\right)
$$
Reject the null hypothesis if this is larger than $\Phi\left(1 - \alpha/p\right)$.
Simulations
Here we perform simple simulations of Bonferroni and corrected Bonferroni.
We will assume that returns are Gaussian, that the correlation follows
our simple rank one form, that the correlation is known in order to perform the
corrected test.
We simulate two years of daily data on 100 assets. For each choice of $\rho$
we perform 10000 simulations under the null of zero SNR, computing the simple and 'improved'
Bonferroni corrected hypothesis tests. We tabulate the empirical type I rate
and plot against $\rho$.
suppressMessages({
library(dplyr)
library(tidyr)
library(future.apply)
})
# set up the functions
rawsim <- function(nday,nlatf,nsim=100,rho=0) {
R <- pmin(diag(nlatf) + rho,1)
mu <- rep(0,nlatf)
apart <- sqrt(nday)/sqrt(1-rho)
bpart <- sqrt(nday) * ((1/sqrt(1-rho+nlatf*rho)) - (1/sqrt(1-rho)))
mhtpvals <- replicate(nsim,{
X <- mvtnorm::rmvnorm(nday,mean=mu,sigma=R)
x <- colMeans(X) / apply(X,2,sd)
bonf_pval <- nlatf * SharpeR::psr(max(x),df=nday-1,zeta=0,ope=1,lower.tail=FALSE)
# do the correction
corr_stat <- apart * max(x) + bpart * mean(x)
corr_pval <- nlatf * pnorm(corr_stat,lower.tail=FALSE)
c(bonf_pval,corr_pval)
})
data_frame(bonf_pvals=as.numeric(mhtpvals[1,]),
corr_pvals=as.numeric(mhtpvals[2,]))
}
many_rawsim <- function(nday,nlatf,rho,nsim=1000L,nnodes=7) {
if ((nsim > 10*nnodes) && require(future.apply)) {
plan(multisession, workers = 7)
nper <- as.numeric(table(1:nsim %% nnodes))
retv <- future_lapply(nper,function(aper) rawsim(nday=nday,nlatf=nlatf,rho=rho,nsim=aper)) %>%
bind_rows()
plan(sequential)
} else {
retv <- rawsim(nday=nday,nlatf=nlatf,rho=rho,nsim=nsim)
}
retv
}
mhtsim <- function(alpha=0.05,...) {
many_rawsim(...) %>%
tidyr::gather(key=method,value=pvalues) %>%
group_by(method) %>%
summarize(rej_rate=mean(pvalues < alpha)) %>%
ungroup() %>%
arrange(method)
}
# perform simulations
nsim <- 10000
nday <- 2*252
nlatf <- 100
params <- data_frame(rho=seq(0.01,0.99,length.out=7))
set.seed(123)
resu <- params %>%
group_by(rho) %>%
summarize(resu=list(mhtsim(nday=nday,nlatf=nlatf,rho=rho,nsim=nsim))) %>%
ungroup() %>%
unnest()
suppressMessages({
library(dplyr)
library(ggplot2)
})
# plot empirical rates:
ph <- resu %>%
mutate(method=gsub('bonf_pvals','Plain Bonferroni',method)) %>%
mutate(method=gsub('corr_pvals','Corrected Bonferroni',method)) %>%
ggplot(aes(rho,rej_rate,color=method)) +
geom_line() + geom_point() +
geom_hline(yintercept=0.05,linetype=2,alpha=0.5) +
scale_y_sqrt() +
labs(title='Empirical type I rate at the 0.05 level',
x=expression(rho),y='type I rate',
color='test')
print(ph)
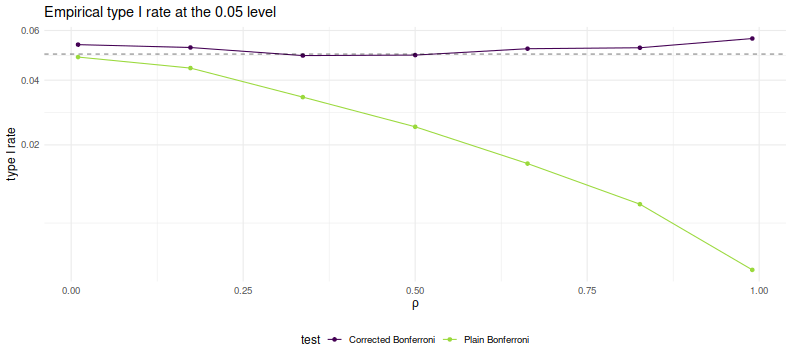
As desired, we maintain nominal coverage using the correction for $\rho$, while
the naive Bonferroni is too conservative for large $\rho$.
This is not yet a practical test, but could be used for rough estimation by
plugging in the average sample correlation (or just SWAG'ing one).
To my tastes a more interesting question is whether one can
generalize this process to a rank $k$ approximation of $R$ while
keeping the monotonicity property. (I have my doubts this is possible)
Click to read and post comments
May 11, 2019
In a previous blog post we looked at a symmetric
confidence intervals on the Signal-Noise ratio.
That study was motivated by the "opportunistic strategy", wherein
one observes the historical returns of an asset to determine whether
to hold it long or short. Then, conditional on the sign of the trade,
we were able to construct proper confidence intervals on the Signal-Noise
ratio of the opportunistic strategy's returns.
I had hoped that one could generalize from the single asset opportunistic
strategy to the case of $p$ assets, where one constructs the Markowitz
portfolio based on observed returns.
I have not had much luck finding that generalization.
However, we can generalize the opportunistic strategy in a different
way to what I call the "Winner Take All" strategy.
Here one observes the historical returns of $p$ different assets,
then chooses the one with the highest observed Sharpe ratio to hold long.
(Let us hold off on an Opportunistic Winner Take All.)
Observe, however, this is just the problem of inferring the Signal Noise
ratio (SNR) of the asset with the maximal Sharpe.
We previously approached that problem using a
Markowitz approximation, finding it somewhat lacking.
That Markowitz approximation was an attempt to correct some deficiencies
with what is apparently the state of the art in the field, Marcos
Lopez de Prado's (now AQR's?) "Most Important Plot in All of Finance",
which is a thin layer of Multiple Hypothesis Testing correction over the
usual distribution of the Sharpe ratio.
In a previous blog post, we found that
Lopez de Prado's method would have lower than nominal type I rates
as it ignored correlation of assets.
Moreover, a simple MHT correction will not, I think,
deal very well with the case where there are great differences
in the Signal Noise ratios of the assets.
The 'stinker' assets with low SNR will simply spoil our inference,
unlikely to have much influence on which asset shows the
highest Sharpe ratio, and only causing us to increase our
significance threshold.
With my superior googling skills I recently discovered a 2013 paper
by Lee et al,
titled Exact Post-Selection Inference, with Application to the Lasso.
While aimed at the Lasso, this paper includes a procedure that
essentially solves our problem, giving hypothesis tests or
confidence intervals with nominal coverage on the asset with
maximal Sharpe among a set of possibly correlated assets.
The Lee et al paper assumes one observes $p$-vector
$$
y \sim \mathcal{N}\left(\mu,\Sigma\right).
$$
Then conditional on $y$ falling in some polyhedron, $Ay \le b$, we wish
to perform inference on $\nu^{\top}y$.
In our case the polyhedron will be the union of all polyhedra with the same
maximal element of $y$ as we observed.
That is, assume that we have reordered the elements of $y$ such that $y_1$ is the
largest element. Then $A$ will be a column of negative ones, cbinded to the $p-1$ identity
matrix, and $b$ will be a $p-1$ vector of zeros.
The test is defined on $\nu=e_1$ the vector with a single one in the first element
and zero otherwise.
Their method works by decomposing the condition $Ay \le b$ into a condition on
$\nu^{\top}y$ and a condition on some $z$ which is normal but independent of
$\nu^{\top}y$.
You can think of this as kind of inverting the transform by $A$.
After this transform, the value of $\nu^{\top}y$ is restricted to a line
segment, so we need only perform inference on a truncated normal.
The code to implement this is fairly straightforward, and given below.
The procedure to compute the quantile function, which we will need
to compute confidence intervals, is a bit trickier, due to numerical
issues. We give a hacky version below.
# Lee et. al eqn (5.8)
F_fnc <- function(x,a,b,mu=0,sigmasq=1) {
sigma <- sqrt(sigmasq)
phis <- pnorm((c(x,a,b)-mu)/sigma)
(phis[1] - phis[2]) / (phis[3] - phis[2])
}
# Lee eqns (5.4), (5.5), (5.6)
Vfuncs <- function(z,A,b,ccc) {
Az <- A %*% z
Ac <- A %*% ccc
bres <- b - Az
brat <- bres
brat[Ac!=0] <- brat[Ac!=0] / Ac[Ac!=0]
Vminus <- max(brat[Ac < 0])
Vplus <- min(brat[Ac > 0])
Vzero <- min(bres[Ac == 0])
list(Vminus=Vminus,Vplus=Vplus,Vzero=Vzero)
}
# Lee et. al eqn (5.9)
ptn <- function(y,A,b,nu,mu,Sigma,numu=as.numeric(t(nu) %*% mu)) {
Signu <- Sigma %*% nu
nuSnu <- as.numeric(t(nu) %*% Signu)
ccc <- Signu / nuSnu # eqn (5.3)
nuy <- as.numeric(t(nu) %*% y)
zzz <- y - ccc * nuy # eqn (5.2)
Vfs <- Vfuncs(zzz,A,b,ccc)
F_fnc(x=nuy,a=Vfs$Vminus,b=Vfs$Vplus,mu=numu,sigmasq=nuSnu)
}
# invert the ptn function to find nu'mu at a given pval.
citn <- function(p,y,A,b,nu,Sigma) {
Signu <- Sigma %*% nu
nuSnu <- as.numeric(t(nu) %*% Signu)
ccc <- Signu / nuSnu # eqn (5.3)
nuy <- as.numeric(t(nu) %*% y)
zzz <- y - ccc * nuy # eqn (5.2)
Vfs <- Vfuncs(zzz,A,b,ccc)
# you want this, but there are numerical issues:
#f <- function(numu) { F_fnc(x=nuy,a=Vfs$Vminus,b=Vfs$Vplus,mu=numu,sigmasq=nuSnu) - p }
sigma <- sqrt(nuSnu)
f <- function(numu) {
phis <- pnorm((c(nuy,Vfs$Vminus,Vfs$Vplus)-numu)/sigma)
#(phis[1] - phis[2]) - p * (phis[3] - phis[2])
phis[1] - (1-p) * phis[2] - p * phis[3]
}
# this fails sometimes, so find a better interval
intvl <- c(-1,1) # a hack.
# this is very unfortunate
trypnts <- seq(from=min(y),to=max(y),length.out=31)
ys <- sapply(trypnts,f)
dsy <- diff(sign(ys))
if (any(dsy < 0)) {
widx <- which(dsy < 0)
intvl <- trypnts[widx + c(0,1)]
} else {
maby <- 2 * (0.1 + max(abs(y)))
trypnts <- seq(from=-maby,to=maby,length.out=31)
ys <- sapply(trypnts,f)
dsy <- diff(sign(ys))
if (any(dsy < 0)) {
widx <- which(dsy < 0)
intvl <- trypnts[widx + c(0,1)]
}
}
uniroot(f=f,interval=intvl,extendInt='yes')$root
}
Testing on normal data
Here we test the code above on the problem considered in Theorem 5.2 of
Lee et al.
That is, we draw
$y \sim \mathcal{N}\left(\mu,\Sigma\right)$,
then observe the value of $F$ given in Theorem 5.2
when we plug in the actual population values of $\mu$ and $\Sigma$.
This is several steps removed from our problem of inference on
the SNR, but it is best to pause and make sure the implementation
is correct first.
We perform 5000 simulations, letting $p=20$, then creating a random $\mu$ and
$\Sigma$, drawing a single $y$, observing which element is the maximum,
creating $A, b, \nu$, then computing the $F$ function, resulting in
a $p$-value which should be uniform. We Q-Q plot those empirical $p$-values
against a uniform law, finding them on the $y=x$ line.
gram <- function(x) { t(x) %*% x }
rWish <- function(n,p=n,Sigma=diag(p)) {
require(mvtnorm)
gram(rmvnorm(p,sigma=Sigma))
}
nsim <- 5000
p <- 20
A1 <- cbind(-1,diag(p-1))
set.seed(1234)
pvals <- replicate(nsim,{
mu <- rnorm(p)
Sigma <- rWish(n=2*p+5,p=p)
y <- t(rmvnorm(1,mean=mu,sigma=Sigma) )
# collect the maximum, so reorder the A above
yord <- order(y,decreasing=TRUE)
revo <- seq_len(p)
revo[yord] <- revo
A <- A1[,revo]
nu <- rep(0,p)
nu[yord[1]] <- 1
b <- rep(0,p-1)
foo <- ptn(y=y,A=A,b=b,nu=nu,mu=mu,Sigma=Sigma)
})
# plot them:
library(dplyr)
library(ggplot2)
ph <- data_frame(pvals=pvals) %>%
ggplot(aes(sample=pvals)) +
geom_qq(distribution=stats::qunif) +
geom_qq_line(distribution=stats::qunif)
print(ph)
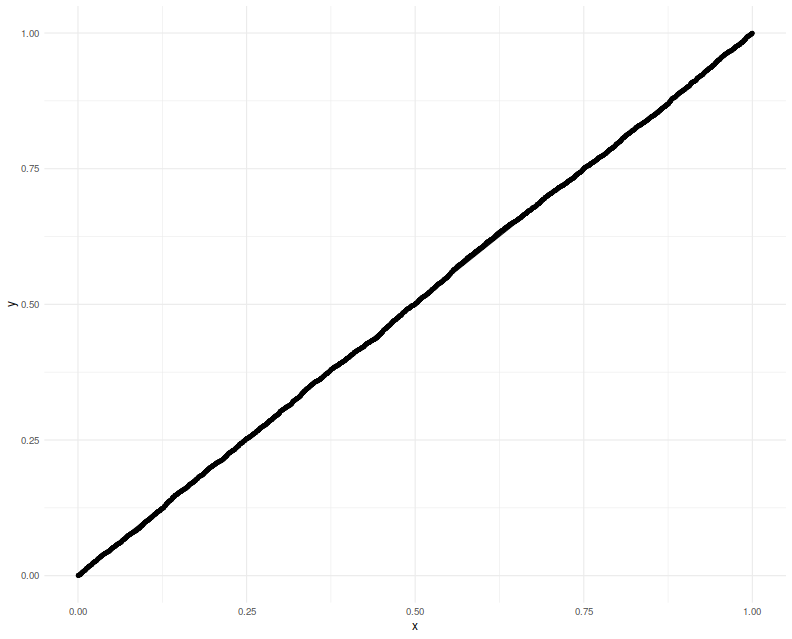
Now we attempt to use the confidence interval code. We construct
a one-sided 95% confidence interval, and check how often it is violated
by the $\mu$ of the element which shows the highest $y$. We will
find that the empirical rate of violations of our confidence interval
is indeed around 5%:
nsim <- 5000
p <- 20
A1 <- cbind(-1,diag(p-1))
set.seed(1234)
tgtval <- 0.95
viols <- replicate(nsim,{
mu <- rnorm(p)
Sigma <- rWish(n=2*p+5,p=p)
y <- t(rmvnorm(1,mean=mu,sigma=Sigma) )
# collect the maximum, so reorder the A above
yord <- order(y,decreasing=TRUE)
revo <- seq_len(p)
revo[yord] <- revo
A <- A1[,revo]
nu <- rep(0,p)
nu[yord[1]] <- 1
b <- rep(0,p-1)
# mu is unknown to this guy
foo <- citn(p=tgtval,y=y,A=A,b=b,nu=nu,Sigma=Sigma)
violated <- mu[yord[1]] < foo
})
print(sprintf('%.2f%%',100*mean(viols)))
Testing on the Sharpe ratio
To use this machinery to perform inference on the SNR, we can either port
the results to the multivariate $t$-distribution,
which seems unlikely because uncorrelated marginals of a multivariate
$t$ are not independent.
Instead we lean on the normal approximation to the vector of Sharpe ratios.
If the $p$-vector $x$ is normal with correlation matrix $R$, then
$$
\hat{\zeta}\approx\mathcal{N}\left(\zeta,\frac{1}{n}\left(
R + \frac{1}{2}\operatorname{Diag}\left(\zeta\right)\left(R \odot R\right)\operatorname{Diag}\left(\zeta\right)
\right)\right),
$$
where $\hat{\zeta}$ is the $p$-vector of Sharpe ratios
computed by observing $n$ independent draws of $x$, and
$\zeta$ is the $p$-vector of Signal Noise ratios.
Note how this generalizes the 'Lo' form of the standard
error of a scalar Sharpe ratio, viz
$\sqrt{(1 + \zeta^2/2)/n}$.
Here we will check the uniformity of $p$ values resulting from
using this normal approximation. This is closer to the actual
inference we want to do, except we will cheat by using the actual $R$ and $\zeta$
to construct what is essentially the $\Sigma$ to Lee's formulation.
We will set $p=20$ and draw 3 years of daily data.
Again we plot the putative $p$-values against uniformity
and find a good match.
# let's test it!
nsim <- 5000
p <- 20
ndays <- 3 * 252
A1 <- cbind(-1,diag(p-1))
set.seed(4321)
pvals <- replicate(nsim,{
# population values here
mu <- rnorm(p)
Sigma <- rWish(n=2*p+5,p=p)
RRR <- cov2cor(Sigma)
zeta <- mu /sqrt(diag(Sigma))
Xrets <- rmvnorm(ndays,mean=mu,sigma=Sigma)
srs <- colMeans(Xrets) / apply(Xrets,2,FUN=sd)
y <- srs
mymu <- zeta
mySigma <- (1/ndays) * (RRR + (1/2) * diag(zeta) %*% (RRR * RRR) %*% diag(zeta))
# collect the maximum, so reorder the A above
yord <- order(y,decreasing=TRUE)
revo <- seq_len(p)
revo[yord] <- revo
A <- A1[,revo]
nu <- rep(0,p)
nu[yord[1]] <- 1
b <- rep(0,p-1)
foo <- ptn(y=y,A=A,b=b,nu=nu,mu=mymu,Sigma=mySigma)
})
# plot them:
library(dplyr)
library(ggplot2)
ph <- data_frame(pvals=pvals) %>%
ggplot(aes(sample=pvals)) +
geom_qq(distribution=stats::qunif) +
geom_qq_line(distribution=stats::qunif)
print(ph)
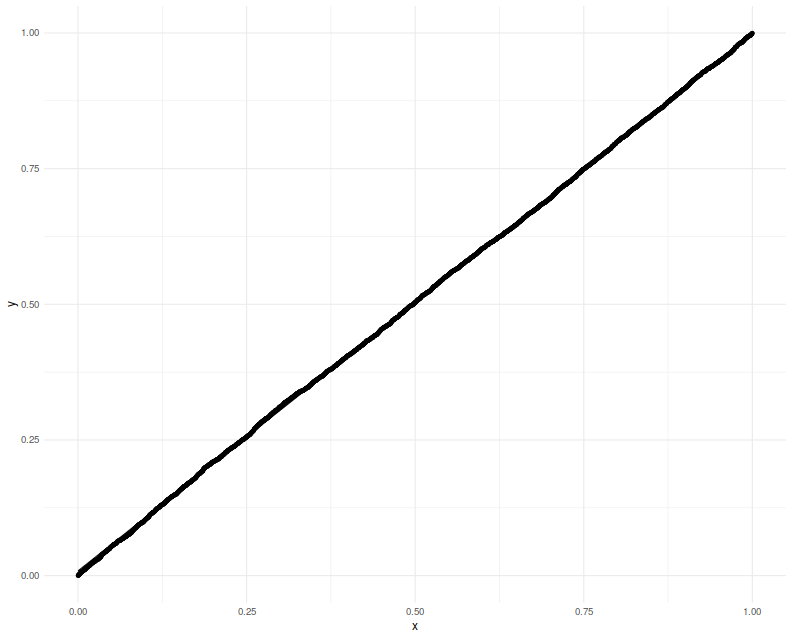
Lastly we make one more modification, filling in
sample estimates for $\zeta$ and $R$ into the computation
of the covariance.
We compute
one-sided 95% confidence intervals, and check how the empirical
rate of violations.
We find the rate to be around 5%.
nsim <- 5000
p <- 20
ndays <- 3 * 252
A1 <- cbind(-1,diag(p-1))
set.seed(9873) # 5678 gives exactly 250 / 5000, which is eerie
tgtval <- 0.95
viols <- replicate(nsim,{
# population values here
mu <- rnorm(p)
Sigma <- rWish(n=2*p+5,p=p)
RRR <- cov2cor(Sigma)
zeta <- mu /sqrt(diag(Sigma))
Xrets <- rmvnorm(ndays,mean=mu,sigma=Sigma)
srs <- colMeans(Xrets) / apply(Xrets,2,FUN=sd)
Sighat <- cov(Xrets)
Rhat <- cov2cor(Sighat)
y <- srs
# now use the sample approximations.
# you can compute this from the observed information.
mySigma <- (1/ndays) * (Rhat + (1/2) * diag(srs) %*% (Rhat * Rhat) %*% diag(srs))
# collect the maximum, so reorder the A above
yord <- order(y,decreasing=TRUE)
revo <- seq_len(p)
revo[yord] <- revo
A <- A1[,revo]
nu <- rep(0,p)
nu[yord[1]] <- 1
b <- rep(0,p-1)
# mu is unknown to this guy
foo <- citn(p=tgtval,y=y,A=A,b=b,nu=nu,Sigma=mySigma)
violated <- zeta[yord[1]] < foo
})
print(sprintf('%.2f%%',100*mean(viols)))
Putting it together
Lee's method appears to give nominal coverage for hypothesis tests and confidence
intervals on the SNR of the asset with maximal Sharpe.
In principle it should not be affected by correlation of the assets
or by large differences in the SNRs of the assets.
It should be applicable in the $p > n$ case, as we are not inverting
the covariance matrix.
On the negative side, requiring one estimate the correlation of assets
for the computation will not scale with large $p$.
We are guardedly optimistic that this method is not adversely affected by the
normal approximation of the Sharpe ratio,
although it would be ill-advised to use it for the case of small samples
until more study is performed.
Moreover the quantile function we hacked together here should be improved
for stability and accuracy.
Click to read and post comments
Mar 17, 2019
Consider the problem of computing confidence intervals on the Signal-Noise
ratio, which is the population quantity $\zeta = \mu/\sigma$,
based on the observed Sharpe ratio $\hat{\zeta} = \hat{\mu}/\hat{\sigma}$.
If returns are Gaussian, one can compute 'exact' confidence intervals
by inverting the CDF of the non-central $t$ distribution with respect
to its parameter.
Typically instead one often uses an approximate standard error, using
either the formula published by Johnson & Welch (and much later by Andrew Lo),
or one using higher order moments given by Mertens, then constructs
Wald-test confidence intervals.
Using standard errors yields symmetric intervals of the
form
$$
\hat{\zeta} \pm z_{\alpha/2} s,
$$
where $s$ is the approximate standard error, and $z_{\alpha/2}$ is the normal $\alpha/2$ quantile.
As typically constructed, the 'exact' confidence intervals based on the non-central $t$
distributionare not symmetric in general, but are very close, and can be made
symmetric. The symmetry condition can be expressed as
$$
\mathcal{P}\left(|\zeta - \hat{\zeta}| \ge c\right) = \alpha,
$$
where $c$ is some constant.
Picking sides
Usually I think of the Sharpe ratio as a tool to answer the
question:
Should I invest a predetermined amount of capital (long) in this asset?
The Sharpe ratio can be used to construct confidence intervals
on the Signal-Noise ratio to help answer that question.
Pretend instead that you are more opportunistic: instead of considering
a predetermined side to the trade, you will observe historical returns
of the asset. Then if the Sharpe ratio is positive, you will consider investing
in the asset, and if the Sharpe is negative, you will consider shorting the
asset. Can we rely on our standard confidence intervals now? After all,
we are now trying to perform inference on
$\operatorname{sign}\left(\hat{\zeta}\right) \zeta$, which is not a population
quantity. Rather it mixes up the population Signal-Noise ratio with
information from the observed sample (the sign of the Sharpe).
(Because of this mixing of a population quantity with information from
the sample, real statisticians
get a bit indignant
when you try to call this a "confidence interval". So don't do that.)
It turns out that you can easily adapt the symmetric confidence intervals
to this problem. Because you can multiply
the inside of $\left|\zeta - \hat{\zeta}\right|$ by $\pm 1$ without
affecting the absolute value, we have
$$
\left|\zeta - \hat{\zeta}\right| \ge c \Leftrightarrow
\left| \operatorname{sign}\left(\hat{\zeta}\right) \zeta - \left|\hat{\zeta}\right|\right| \ge c.
$$
Thus
$$
\left|\hat{\zeta}\right| \pm z_{\alpha/2} s
$$
are $1-\alpha$ confidence intervals on
$\operatorname{sign}\left(\hat{\zeta}\right) \zeta$.
Although the type I error rate is maintained, the 'violations' of the
confidence interval can be asymmetric.
When the Signal Noise ratio is large (in absolute value), type I errors
tend to occur on both sides of the confidence interval equally, because
the Sharpe is usually the same sign as the Signal-Noise ratio.
When the Signal-Noise ratio is near zero, however, typically the type I
errors occur only on the lower side.
(This must be the case when the Signal-Noise ratio is exactly zero.)
Of course, since the Signal-Noise ratio is the unknown population parameter,
you do not know which situation you are in, although you have some
hints from the observed Sharpe ratio.
Before moving on, here we test the symmetric confidence intervals.
We vary the Signal Noise ratio from 0 to 2.5 in 'annual units',
draw two years of daily normal returns with that Signal-Noise ratio,
pick a side of the trade based on the sign of the Sharpe ratio,
then build symmetric confidence intervals using the standard
error estimator $\sqrt{(1 + \hat{\zeta}^2/2)/n}$.
We build the 95% confidence intervals, then note any
breaches of the upper and lower confidence bounds.
We repeat this 10000 times for each choice of SNR.
We then plot the type I rate for the lower bound of the CI, the upper
bound and the total type I rate, versus the Signal Noise ratio.
We see that the total empirical type I rate is very near the nominal
rate of 5%, and this is entirely attributable to violations of
the lower bound up until a Signal Noise ratio of around 1.4 per
square root year. At around 2.5 per square root year, the type I errors
are observed in equal proportion on both sides of the CI.
suppressMessages({
library(dplyr)
library(tidyr)
library(future.apply)
})
# run one simulation of normal returns and CI violations
onesim <- function(n,pzeta,zalpha=qnorm(0.025)) {
x <- rnorm(n,mean=pzeta,sd=1)
sr <- mean(x) / sd(x)
se <- sqrt((1+0.5*sr^2)/n)
cis <- abs(sr) + se * abs(zalpha) * c(-1,1)
pquant <- sign(sr) * pzeta
violations <- c(pquant < cis[1],pquant > cis[2])
}
# do a bunch of sims, then sum the violations of low and high;
repsim <- function(nrep,n,pzeta,zalpha) {
jumble <- replicate(nrep,onesim(n=n,pzeta=pzeta,zalpha=zalpha))
retv <- t(jumble)
colnames(retv) <- c('nlo','nhi')
retv <- as.data.frame(retv) %>%
summarize_all(.funs=sum)
retv$nrep <- nrep
invisible(retv)
}
manysim <- function(nrep,n,pzeta,zalpha,nnodes=7) {
if (nrep > 2*nnodes) {
plan(multisession, workers = 7)
# do in parallel.
nper <- table(1 + ((0:(nrep-1) %% nnodes)))
retv <- future_lapply(nper,function(aper) repsim(nrep=aper,n=n,pzeta=pzeta,zalpha=zalpha)) %>%
bind_rows() %>%
summarize_all(.funs=sum)
plan(sequential)
} else {
retv <- repsim(nrep=nrep,n=n,pzeta=pzeta,zalpha=zalpha)
}
# turn sums into means
retv %>%
mutate(vlo=nlo/nrep,vhi=nhi/nrep) %>%
dplyr::select(vlo,vhi)
}
# run a bunch
ope <- 252
nyr <- 2
alpha <- 0.05
# simulation params
params <- data_frame(zetayr=seq(0,2.5,by=0.0625)) %>%
mutate(pzeta=zetayr/sqrt(ope)) %>%
mutate(n=round(ope*nyr))
# run a bunch
nrep <- 100000
set.seed(4321)
system.time({
results <- params %>%
group_by(zetayr,pzeta,n) %>%
summarize(sims=list(manysim(nrep=nrep,nnodes=7,
pzeta=pzeta,n=n,zalpha=qnorm(alpha/2)))) %>%
ungroup() %>%
tidyr::unnest()
})
suppressMessages({
library(dplyr)
library(tidyr)
library(ggplot2)
})
ph <- results %>%
mutate(vtot=vlo+vhi) %>%
gather(key=series,value=violations,vlo,vhi,vtot) %>%
mutate(series=case_when(.$series=='vlo' ~ 'below lower CI',
.$series=='vhi' ~ 'above upper CI',
.$series=='vtot' ~ 'outside CI',
TRUE ~ 'error')) %>%
ggplot(aes(zetayr, violations, colour=series)) +
geom_line() + geom_point(alpha=0.5) +
geom_hline(yintercept=c(alpha/2,alpha),linetype=2,alpha=0.5) +
labs(x='SNR (per square root year)',y='type I rate',
color='error type',title='Rates of type I error when trade side is sign of Sharpe')
print(ph)
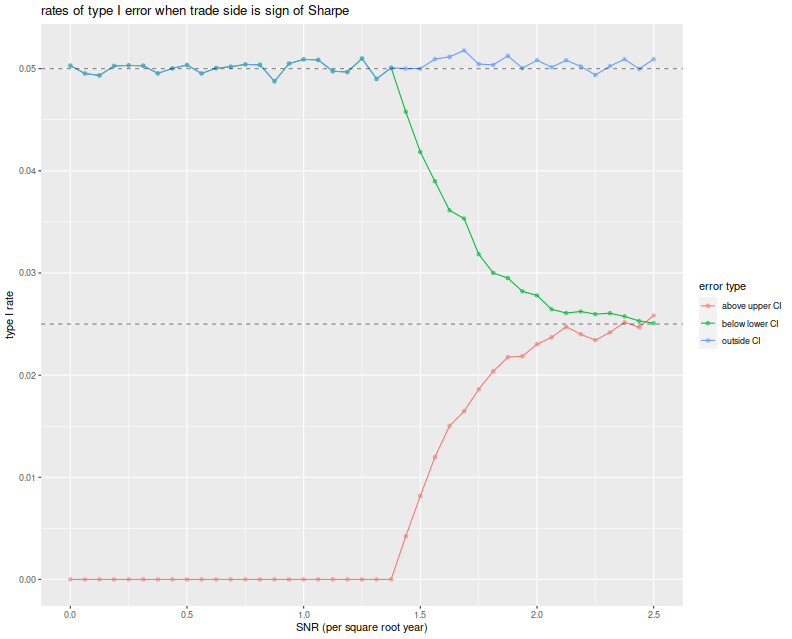
A Bayesian Donut?
Of course, this strategy seems a bit unrealistic:
what's the point of constructing confidence intervals if you are
going to trade the asset no matter what the evidence?
Instead, consider a fund manager whose trading strategies are
all above average: she/he observes the Sharpe ratio of a backtest,
then only trades a strategy if $|\hat{\zeta}| \ge c$ for some sufficiently
large $c$, and picks a side based on $\operatorname{sign}\left(\hat{\zeta}\right)$.
This is a 'donut'.
Conditional on observing $|\hat{\zeta}| \ge c$, can one construct
a reliable confidence interval on
$\operatorname{sign}\left(\hat{\zeta}\right) \zeta$?
Perhaps our fund manager thinks there is no point in doing so if $c$
is sufficiently large.
I think to do so you have to make some assumptions about the distribution of $\zeta$
and rely on Baye's law.
We did not say what would happen if the junior quant at this shop
developed a strategy where $|\hat{\zeta}| < c$, but presumably
the junior quants were told to keep working until they beat the magic
threshold.
If the junior quants only produce strategies with small $\zeta$, one
suspects that the $c$ threshold does very little to reject bad
strategies, rather it just slows down their deployment.
(In response the quants will surely beef up their backtesting
infrastructure, or invent automatic strategy generation.)
Generalizing to higher dimensions
The real interesting question is what this looks like in higher dimensions.
Now one observes $p$ assets, and is to construct a portfolio
on those assets. Can we construct good confidence intervals on the
Sharpe ratio of the chosen portfolio?
In this setting we have many more possible choices, so a general
purpose analysis seems unlikely.
However, if we restrict ourselves to the Markowitz portfolio,
I suspect some progress can be made.
(Although I have been very slow to make it!)
I hope to purse this in a followup blog post.
Click to read and post comments



