Sharpe Ratio

A Sharper Sharpe, Again

Previously on this blog we had performed a fair amount of testing of the "drawdown-based estimator" of the signal-noise ratio, as proposed by Damien Challet. All that analysis was based on the 1.1 version of the sharpeRratio package, written by Challet himself. There was a bug (or bugs) in that package that caused the estimator to be biased, which could also appear as improved efficiency over the traditional "moment-based" estimator due to Sharpe (or Gosset, rather) via shrinkage to zero. Here we analyze the 1.2 version of the package, which presumably fixes this issue.

Checking for bias

Here I perform some simulations to check for bias of the estimator. I draw 128 days of daily returns from a \(t\) distribution with \(\nu=4\) degrees of freedom. I then compute: the moment-based Sharpe ratio; the moment-based Sharpe ratio, but debiased using higher order moments; the drawdown estimator from the 1.2 version of the package; the drawdown estimator from the 1.2 version of the package, but feeding \(\nu\) to the estimator. I do this for many draws of returns. I repeat for 256 days of data, and for the population Signal-Noise ratio varying from 0.30 to 1.5 in "annualized units" (per square root year), assuming 252 trading days per year. I use doFuture to run the simulations in parallel.

suppressMessages({
  library(dplyr)
  library(tidyr)
  library(tibble)
  library(SharpeR)
  library(sharpeRratio)
  # https://cran.r-project.org/web/packages/doFuture/vignettes/doFuture.html
  library(doFuture)
  registerDoFuture()
  plan(multiprocess)
})
# only works for scalar pzeta:
onesim <- function(nday,pzeta=0.1,nu=4) {
  x <- pzeta + sqrt(1 - (2/nu)) * rt(nday,df=nu)
    srv <- SharpeR::as.sr(x,higher_order=TRUE)
    # mental note: this is much more awkward than it should be,
    # let's make it easier in SharpeR!
    #ssr <- mean(x) / sd(x)
    # moment based:
    ssr <- srv$sr
    # debiased
    ssr_b <- ssr - SharpeR::sr_bias(snr=ssr,n=nday,cumulants=srv$cumulants)

    sim <- sharpeRratio::estimateSNR(x)
    # this cheats and gives the true nu to the estimator
    cht <- sharpeRratio::estimateSNR(x,nu=nu)
    c(ssr,ssr_b,sim$SNR,cht$SNR)
}
repsim <- function(nrep,nday,pzeta=0.1,nu=4) {
  dummy <- invisible(capture.output(jumble <- replicate(nrep,onesim(nday=nday,pzeta=pzeta,nu=nu)),file='/dev/null'))
  retv <- t(jumble)
  colnames(retv) <- c('sr','sr_unbiased','ddown','ddown_cheat')
    invisible(as.data.frame(retv))
}
manysim <- function(nrep,nday,pzeta,nu=4,nnodes=5) {
  if (nrep > 2*nnodes) {
    # do in parallel.
    nper <- table(1 + ((0:(nrep-1) %% nnodes))) 
    retv <- foreach(i=1:nnodes,.export = c('nday','pzeta','nu')) %dopar% {
      repsim(nrep=nper[i],nday=nday,pzeta=pzeta,nu=nu)
    } %>%
      bind_rows()
  } else {
    retv <- repsim(nrep=nrep,nday=nday,pzeta=pzeta,nu=nu)
  }
  retv 
}
# summarizing function
sim_summary <- function(retv) {
    retv %>%
        tidyr::gather(key=metric,value=value,-pzeta,-nday) %>%
        filter(!is.na(value)) %>%
        group_by(pzeta,nday,metric) %>%
        summarize(meanvalue=mean(value),
                            serr=sd(value) / sqrt(n()),
                            rmse=sqrt(mean((pzeta - value)^2)),
                            nsims=n()) %>%
        ungroup() %>%
        arrange(pzeta,nday,metric)
}

ope <- 252
pzeta <- seq(0.30,1.5,by=0.30) / sqrt(ope)

params <- tidyr::crossing(tibble::tribble(~nday,128,256),
                          tibble::tibble(pzeta=pzeta))

nrep <- 1000
set.seed(1234)
system.time({
    results <- params %>%
        group_by(nday,pzeta) %>%
            summarize(sims=list(manysim(nrep=nrep,nnodes=7,pzeta=pzeta,nday=nday))) %>%
        ungroup() %>%
        tidyr::unnest(cols=c(sims))
})

   user  system elapsed 
980.530 561.801 199.306 

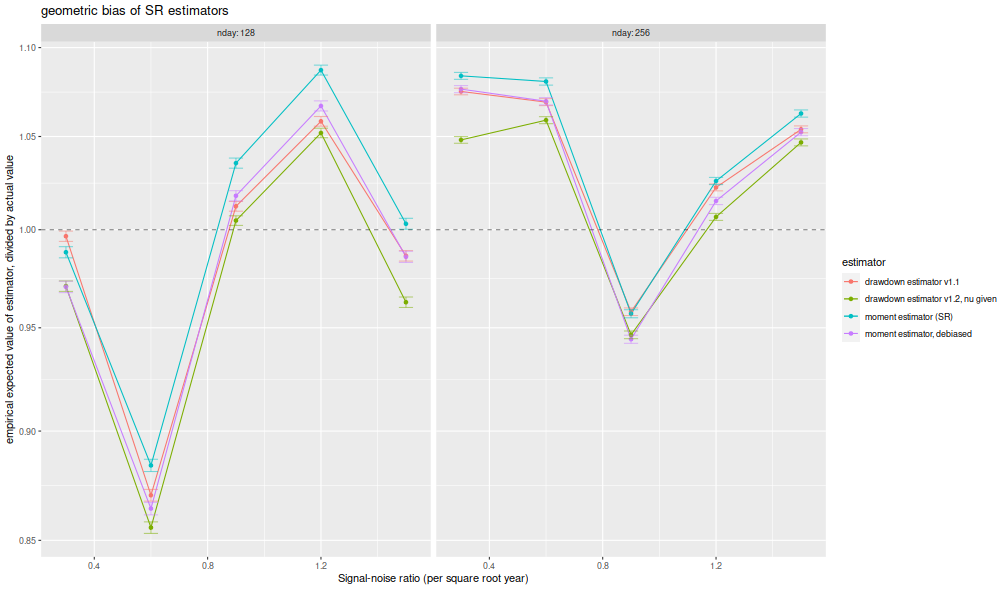
I compute the mean of each estimator over the 1,000 draws, divide that mean estimate by the true Signal-Noise Ratio, then plot versus the annualized SNR. I plot errobars at plus and minus one standard error around the mean. The ratio should be one, any deviation from which is geometric bias in the estimator. Previously this plot showed the drawdown estimator consistently estimating a value around 70% of the true value, a problem which seems to have been fixed, as it now shows values around 95% of the true value. The moment estimator shows a slight positive bias, which is decreasing in sample size, as described by Bao and Miller and Gehr. The higher order moment correction mitigates this effect somewhat for the moment estimator.

library(ggplot2)
ph <- results %>% 
  sim_summary() %>%
  mutate(metric=case_when(.$metric=='ddown' ~ 'drawdown estimator v1.1',
                          .$metric=='ddown_two' ~ 'drawdown estimator v1.2',
                          .$metric=='ddown_cheat' ~ 'drawdown estimator v1.2, nu given',
                          .$metric=='sr_unbiased' ~ 'moment estimator, debiased',
                          .$metric=='sr' ~ 'moment estimator (SR)',
                          TRUE ~ 'error')) %>%
  mutate(bias = meanvalue / pzeta,
         zeta_pa=sqrt(ope) * pzeta,
         serr = serr) %>%
  ggplot(aes(zeta_pa,bias,color=metric,ymin=bias-serr,ymax=bias+serr)) + 
  geom_line() + geom_point() + geom_errorbar(alpha=0.5,width=0.05) + 
  geom_hline(yintercept=1,linetype=2,alpha=0.5) + 
  facet_wrap(~nday,labeller=label_both) +
  scale_y_log10() + 
  labs(x='Signal-noise ratio (per square root year)',
       y='empirical expected value of estimator, divided by actual value',
       color='estimator',
       title='geometric bias of SR estimators')
print(ph)

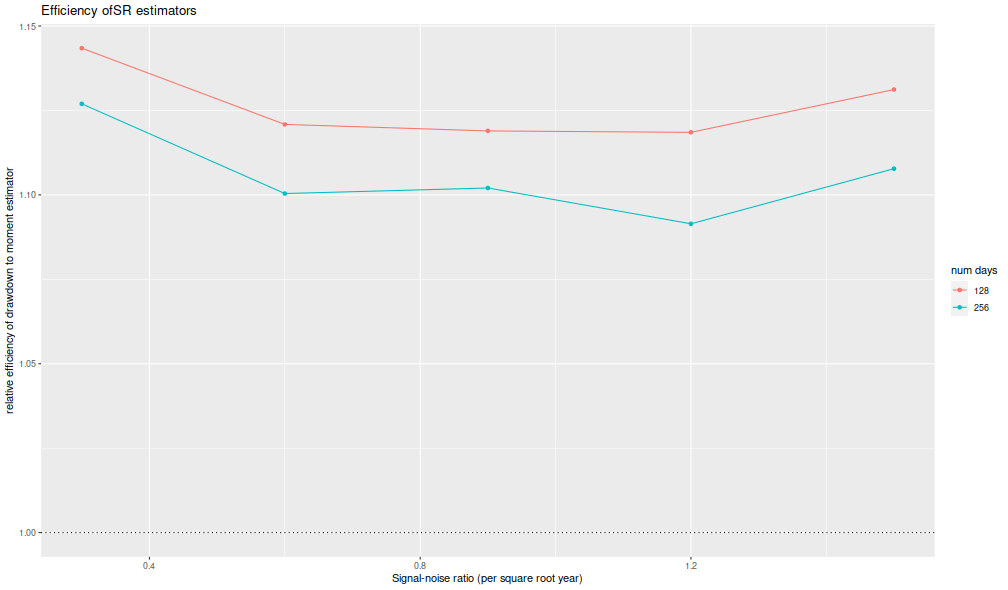
I now plot the 'relative efficiency' as in Figure 4 of version 6 of Challet's paper. This is the ratio of the mean square error of the moment-estimator to the mean square error of the drawdown-estimator, again as a function of the true (annualized) signal-noise ratio, with different lines for the number of days simulated. Challet's plot shows this line as approximately 5, while we see values of around 1.25 or so. That is, we see only modest improvements in efficiency for the drawdown estimator, and not the putative huge gains in efficiency in the paper.

library(ggplot2)
ph <- results %>% 
  sim_summary() %>%
  filter(metric %in% c('sr','ddown')) %>%
  dplyr::select(-meanvalue,-serr,-nsims) %>%
  tidyr::spread(key=metric,value=rmse) %>%
  mutate(eff=(sr/ddown)^2) %>%
  mutate(zeta_pa=sqrt(ope) * pzeta) %>%
  ggplot(aes(zeta_pa,eff,color=factor(nday))) + 
  geom_line() + geom_point() + 
  geom_hline(yintercept=1,linetype=3) + 
  labs(x='Signal-noise ratio (per square root year)',
       y='relative efficiency of drawdown to moment estimator',
       color='num days',
       title='Efficiency ofSR estimators')
print(ph)

Thus it appears that the 1.2 version of the package fixes the bias issues in the initial release.

A Sharper Sharpe: Its Biased.

Note: This blog post previously analyzed Damien Challet's 'Sharper estimator' of the Signal-Noise Ratio. In a series of blog posts, I had found that the implementation of this estimator appeared to be biased, giving perhaps illusory gains in efficiency. I had noted in this post that I contacted Challet to present my concerns about his code. Since the time I wrote that post, Challet updated his sharpeRratio, package to version 1.2. We will perform an investigation of the fixed drawdown estimator, and link to it here.

A Sharper Sharpe: Just Shrink it!

Note: This blog post previously analyzed Damien Challet's 'Sharper estimator' of the Signal-Noise Ratio. Following up on some suspicions, we compared the drawdown estimator to a shrunk version of the moment-based estimator, and found them to have similar performance. However, the analysis used version 1.1 of the sharpeRratio, written by Challet. That version of the package contained a bug which severely biased the estimator, causing illusory improvements in the achieved standard error. Challet has fixed the package, which is now at version 1.2 (or later), and thus the analysis that was here can no longer be reproduced. We will perform an investigation of the fixed drawdown estimator, and link to it here.

A Sharper Sharpe III : MLEs

Note: This blog post previously analyzed Damien Challet's 'Sharper estimator' of the Signal-Noise Ratio. We found that this drawdown estimator seemed empirically to have lower MSE than the Cramér Rao Lower Bound when used to estimate the mean of some distributions, which was a warning that something was wrong. The analysis used version 1.1 of the sharpeRratio, written by Challet. That version of the package contained a bug which severely biased the estimator, causing illusory improvements in the achieved standard error. Challet has fixed the package, which is now at version 1.2 (or later), and thus the analysis that was here can no longer be reproduced. We will perform an investigation of the fixed drawdown estimator, and link to it here.